Introduction
Our oceans are being threatened by growing and severe plastic pollution. Because of its environmental and economic relevance, the reduction of ocean pollution has been listed as an explicit target in the United Nations’ Sustainable Development Goal #14 ‘Life Below Water’. To reduce the legacy floating ocean plastic, our NGO partner, The Ocean Cleanup (TOC), developed a plastic cleaning system that includes a floating barrier dragged by two ships (see video below). The system moves slowly through the water to capture new plastic and needs to empty its retention zone (extraction) regularly. In our paper, we optimize the route and the extraction schedule of their plastic collection system in the ocean to maximize the quantity of plastic collected over time.
Graph-based model & path-dependency structure
In our problem, we discretize the space and time and model the routing and scheduling decisions as paths in a directed acyclic graph (DAG). Under this lens, the quantity of plastic collected can be seen as edge length in this graph and our problem as a longest path optimization problem. However, due to the direct impact of our routing decisions on future plastic density, our resulting optimization problem is a non-linear and non-decomposable longest path problem.
In our paper, we formally analyze the structure of path-dependent edge lengths, which resembles structure arising in covering problems. We derive lower and upper bounds on the estimation error obtained when ignoring the path dependency, which will serve as the basis for our algorithmic strategy.
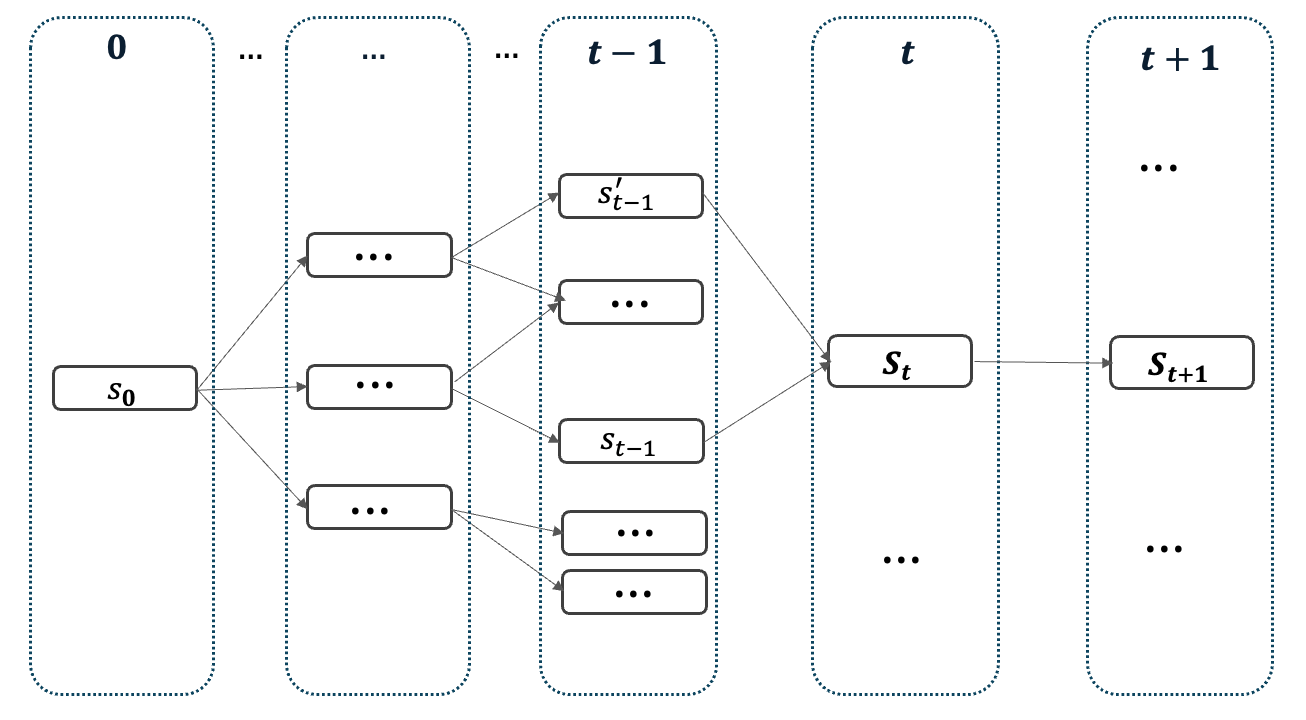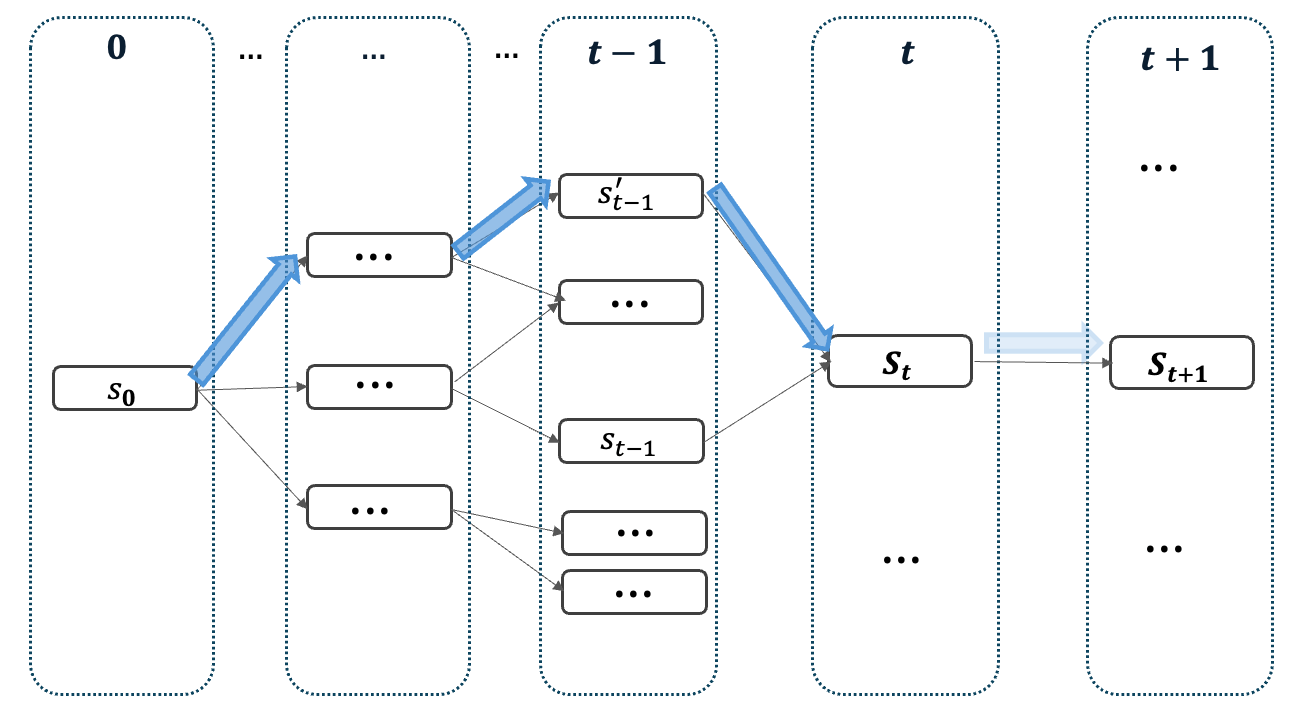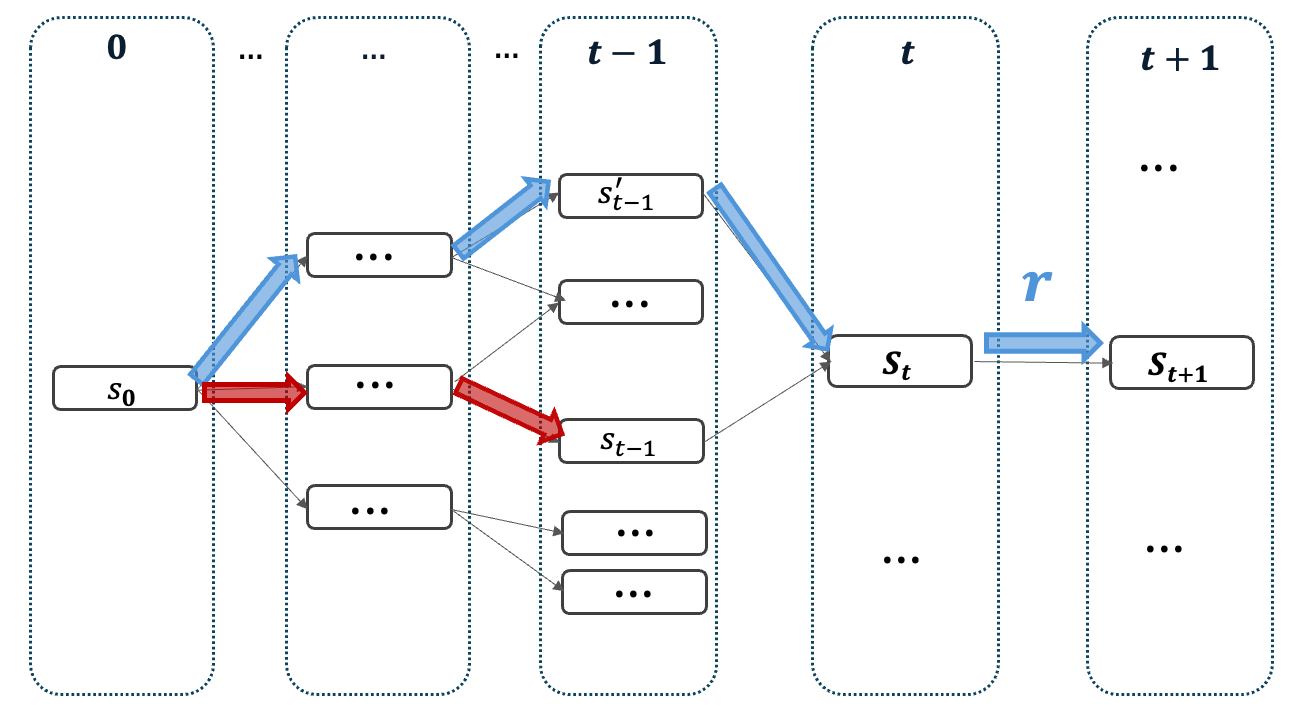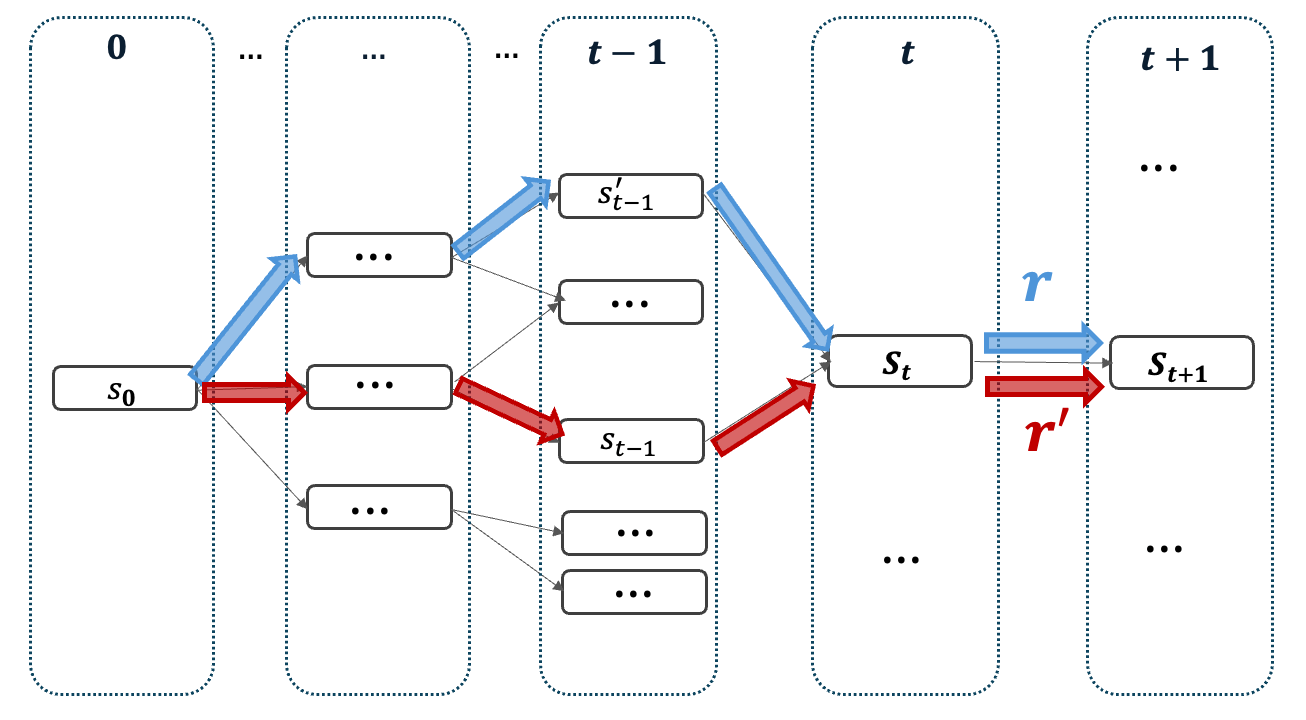
Algorithms
With the analysis of the path-dependency structure, we propose a search-and-bound strategy to efficiently find a high-quality solution for this class of problems, with certificates of near-optimality. Our algorithm leverages a linear relaxation of the problem solvable via dynamic programming to efficiently search through the space of trajectories by combining geographical clustering with terminal values of the DP approach. We also propose a tailored branch-and-bound scheme to solve this class of problems exactly.
Numerical results
We evaluate the benefit of our search-and-bound algorithm on a one-year dataset of ocean weather conditions and plastic density. We find that our optimization approach yields at least a 60% improvement in terms of average collection efficiency compared with their current routing strategy. In particular, we observe greater benefits (+100%) during winter months, because weather conditions (and wave height in particular) are limiting the ability to extract, hence exacerbating the benefit of jointly optimizing the route and the extraction schedule. In addition, our algorithm allows The Ocean Cleanup to explore the non-linear impact of strategic system dimensioning decisions (e.g., span of the system and size of the retention zone).
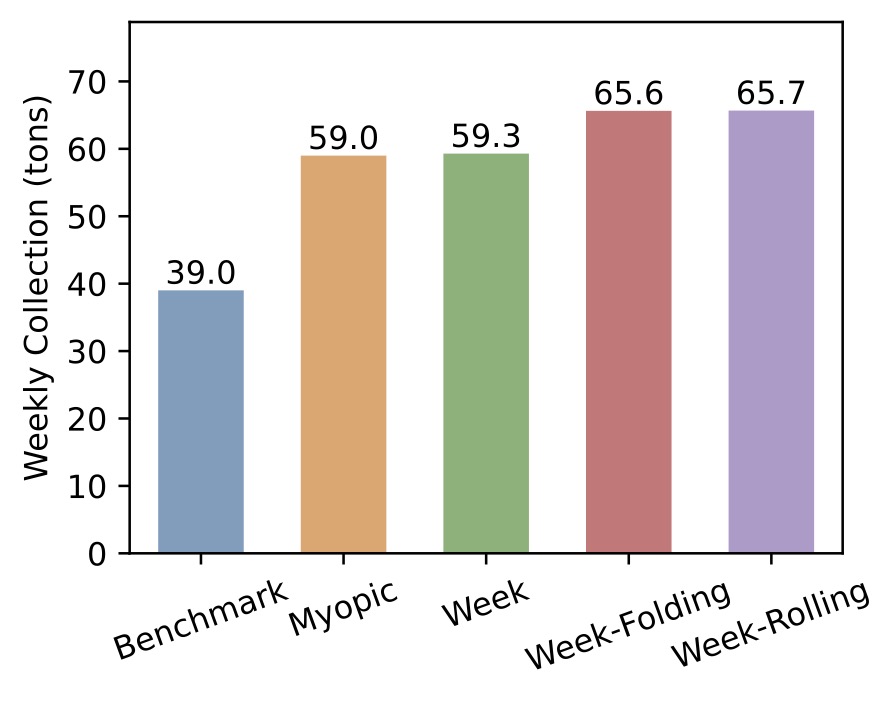
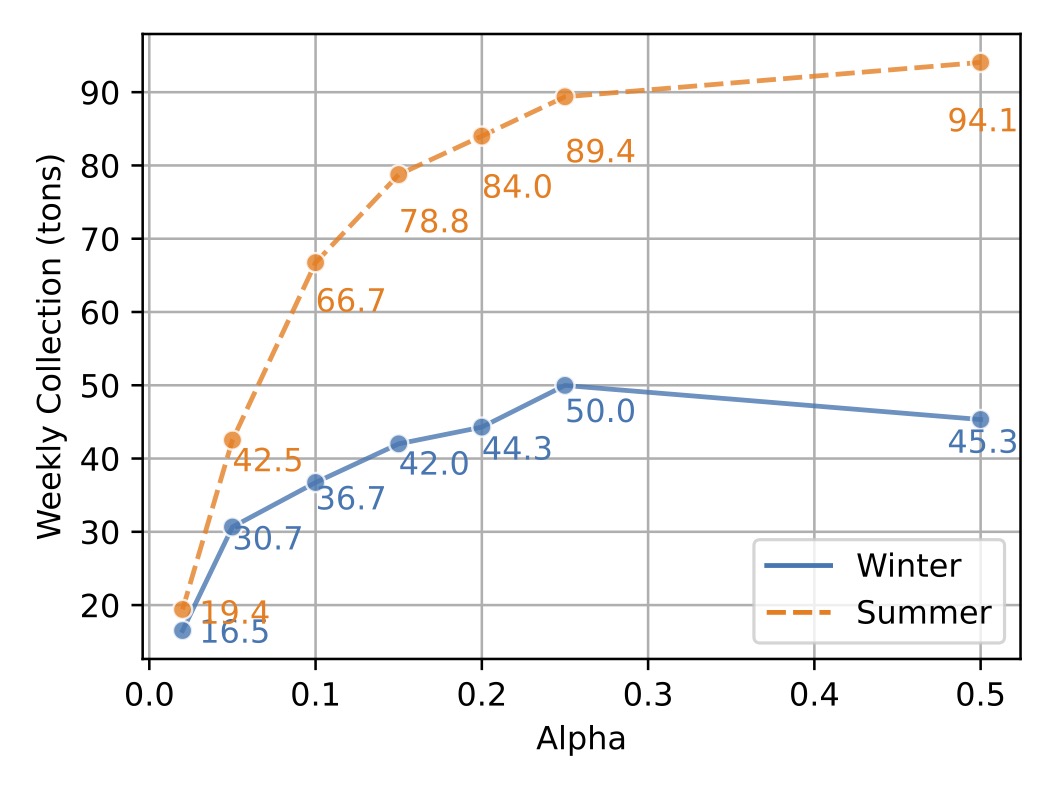
Conclusion
To reduce ocean plastic pollution, we collaborated with The Ocean Cleanup and improve the collection yield of their plastic collection system in the ocean. Specifically, we optimize the route of their plastic collection system to maximize the quantity of plastic collected over time. We formulated this problem as a longest path problem with non-linear polynomial edge lengths, and proposed a search-and-bound method to to efficiently find high-quality solutions. Our method effectively improve their collection effiency, and also informs the design of their next generation system. Looking ahead, it is valuable to account for uncertainty in weather predictions and plastic dynamics. In particular, we are currently investigating whether collection of real-world data by drones or satellites could help quantify uncertainty and lead to robust versions of our longest path problem.


Paper:
- Optimizing the Path Towards Plastic-Free Oceans, Dick den Hertog, Jean Pauphilet, Yannick Pham, Bruno Sainte-Rose, and Baizhi Song (2025). Operations Research, 73(3), 1165-1183.
